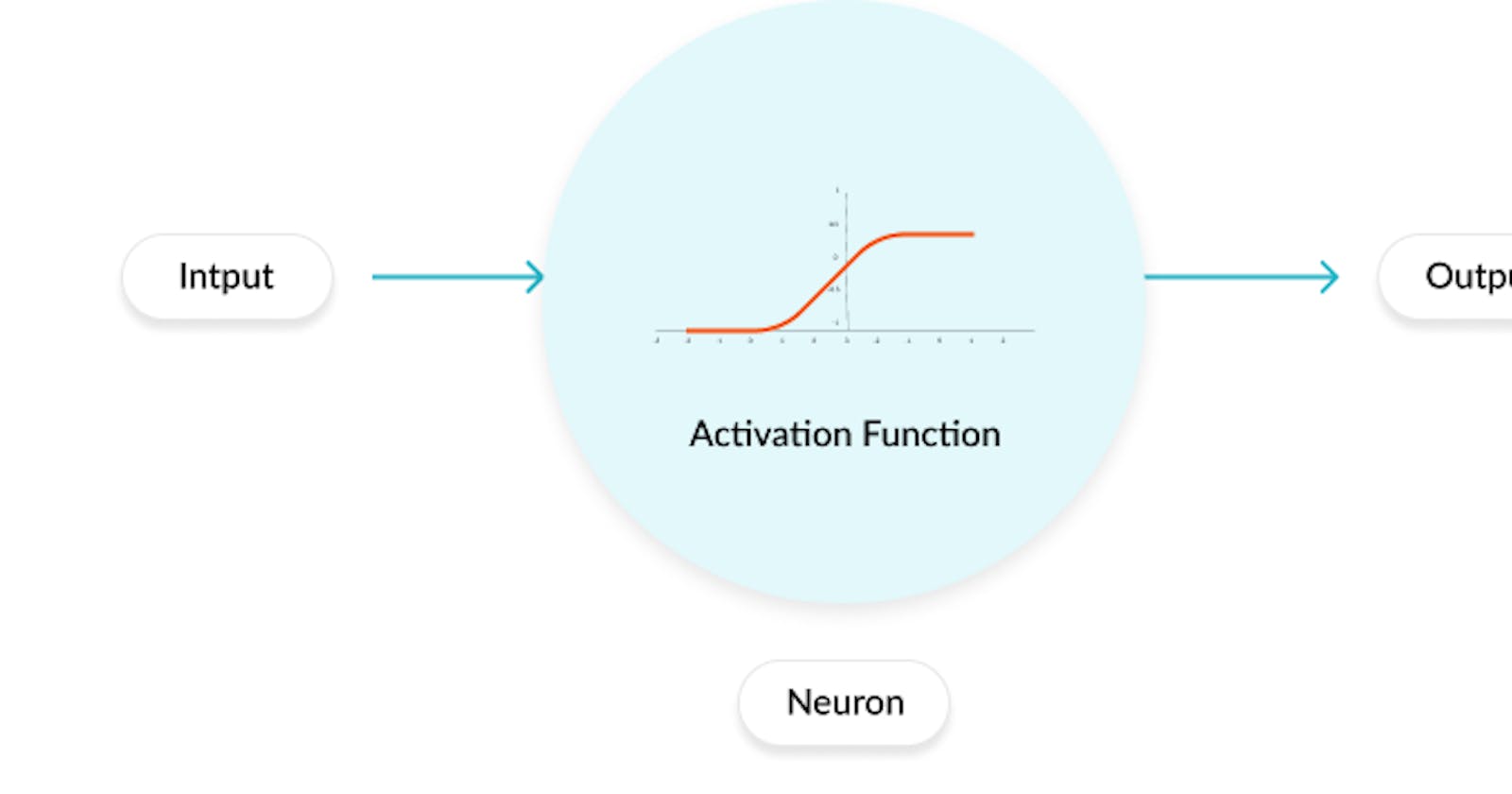
Activation functions are mathematical equations that determine the output of a neural network. The function is attached to each neuron in the network, and determines whether it should be activated (“fired”) or not, based on whether each neuron’s input is relevant for the model’s prediction. Activation functions also help normalize the output of each neuron to a range between 1 and 0 or between -1 and 1.
An additional aspect of activation functions is that they must be computationally efficient because they are calculated across thousands or even millions of neurons for each data sample. Modern neural networks use a technique called backpropagation to train the model, which places an increased computational strain on the activation function, and its derivative function.
From < Link >
Role of the Activation Function in a Neural Network Model
In a neural network, numeric data points, called inputs, are fed into the neurons in the input layer. Each neuron has a weight, and multiplying the input number with the weight gives the output of the neuron, which is transferred to the next layer.
The activation function is a mathematical “gate” in between the input feeding the current neuron and its output going to the next layer. It can be as simple as a step function that turns the neuron output on and off, depending on a rule or threshold. Or it can be a transformation that maps the input signals into output signals that are needed for the neural network to function.
From < Link >
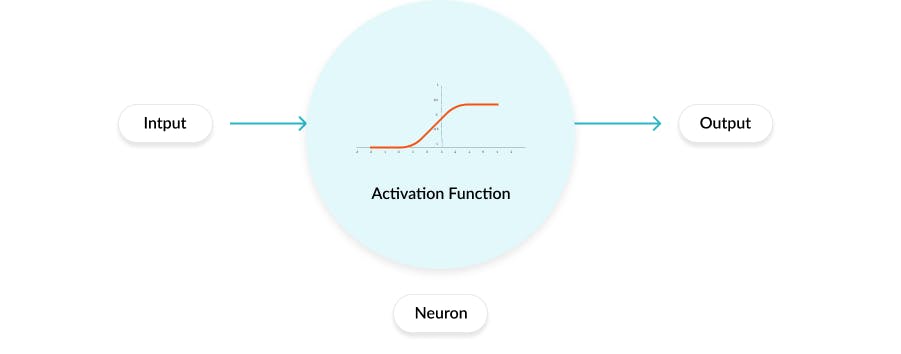
Increasingly, neural networks use non-linear activation functions, which can help the network learn complex data, compute and learn almost any function representing a question, and provide accurate predictions.
The basic process carried out by a neuron in a neural network is:
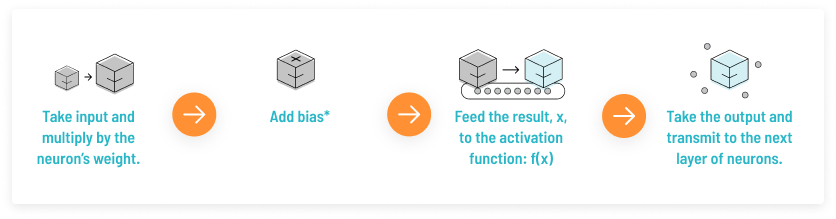
The basic process carried out by a neuron in a neural network * This is just the number 1, making it possible to represent activation functions that do not cross the origin. Biases are also assigned a weight.
From < Link >